The Physics of Colliding-Beam Experiments


In a colliding-beam experiment two beams of
high-energy particles are made to cross each other.
Since the collision occurs at relativistic speeds,
the relevant measure of available energy is the center-of-mass frame.
For colliding beams, this is
( 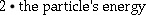 )
if the particles collide with equal and opposite momenta.
)
if the particles collide with equal and opposite momenta.
For a fixed target, it is
 for a high-energy particle colliding with a target particle of mass "m."
for a high-energy particle colliding with a target particle of mass "m."
Imagine that you
double the energy input for both types of collisions.
What is the corresponding rise in available energy (the output)?

-
 The colliding-beam energy goes from
The colliding-beam energy goes from
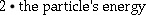 to
to
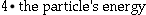 .
So, if you double the energy of the colliding beams,
you get double the collision energy.
.
So, if you double the energy of the colliding beams,
you get double the collision energy.

-
 On the other hand, the fixed-target energy goes from
On the other hand, the fixed-target energy goes from
 to
to
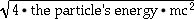 .
Doubling the beam's energy in a fixed-target experiment only results in a
.
Doubling the beam's energy in a fixed-target experiment only results in a
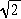 rise of available energy.
rise of available energy.
 From this, it is obvious that
colliding beams are much more efficient than
fixed targets at getting high-energy collisions.
From this, it is obvious that
colliding beams are much more efficient than
fixed targets at getting high-energy collisions.
 Question:
If you have two beams with energy = 50 GeV for a
colliding-beam collision, what energy is need for a
fixed-target collision with
a proton target
(
Question:
If you have two beams with energy = 50 GeV for a
colliding-beam collision, what energy is need for a
fixed-target collision with
a proton target
(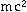 = 1 GeV) to get the same available energy?
= 1 GeV) to get the same available energy?
![]() )
if the particles collide with equal and opposite momenta.
)
if the particles collide with equal and opposite momenta.
![]() for a high-energy particle colliding with a target particle of mass "m."
for a high-energy particle colliding with a target particle of mass "m."