Q348: Optimal Array Multiplication Sequence

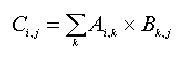
給你2個矩陣A、B，我們使用標準的矩陣相乘定義C=AB如下：

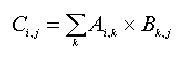
A陣列中欄（column）的數目一定要等於B陣列中列（row）的數目才可以做此2陣列的相乘。若我們以rows(A)，columns(A)分別代表A陣列中列及欄的數目，要計算C陣列共需要的乘法的數目為：rows(A)*columns(B)*columns(A)。例如：A陣列是一個10x20的矩陣，B陣列是個20x15的矩陣，那麼要算出C陣列需要做10*15*20，也就是3000次乘法。

要計算超過2個以上的矩陣相乘就得決定要用怎樣的順序來做。例如：X、Y、Z都是矩陣，要計算XYZ的話可以有2種選擇：(XY)Z 或者 X(YZ)。假設X是5x10的陣列，Y是10x20的陣列，Z是20x35的陣列，那個不同的運算順序所需的乘法數會有不同：

(XY)Z

• 5*20*10 = 1000次乘法完成(XY)，並得到一5x20的陣列。
• 5*35*20 = 3500次乘法得到最後的結果。
• 總共需要的乘法的次數：1000+3500=4500。

X(YZ)

• 10*35*20 = 7000次乘法完成(YZ)，並得到一10x35的陣列。
• 5*35*10 = 1750次乘法得到最後的結果。
• 總共需要的乘法的次數：7000+1750=8750。

很明顯的，我們可以知道計算(XY)Z會使用較少次的乘法。

這個問題是：給你一些矩陣，你要寫一個程式來決定該如何相乘的順序，使得用到乘法的次數會最少。

Input

含有多組測試資料，每組測試資料的第一列，含有1個整數N（N <= 10）代表有多少個陣列要相乘。接下來有N對整數，代表一陣列的列數及欄數。這N個陣列的順序與要你相乘的陣列順序是一樣的。

N=0代表輸入結束。請參考Sample Input。

Output

每組測試資料輸出一列，內容為矩陣相乘的順序（以刮號來表示）使得所用的乘法次數最小。如果有不只一組答案，輸出任一組均可。請參考Sample Output。

Sample Input

3
1 5
5 20
20 1
3
5 10
10 20
20 35
6
30 35
35 15
15 5
5 10
10 20
20 25
0

Sample Output

Case 1: (A1 x (A2 x A3))
Case 2: ((A1 x A2) x A3)
Case 3: ((A1 x (A2 x A3)) x ((A4 x A5) x A6))